定点数和浮点数

发表于 更新于 分类于 本文字数： 2.6k 阅读时长 ≈ 26 分钟

前言

在说定点数和浮点数之前，先回顾一下，整数和小数在计算机怎么表示——二进制形式。

进制计数制

生活中常见的是十进制，那么在计算机中，常见的进制：

  1. 二进制（B，binary），基本符号0、1
  2. 八进制（O，Octal），基本符号0、1、2、3、4、5、6、7
  3. 十进制（D，Decimal），基本符号0、1、2、3、4、5、6、7、8、9
  4. 十六进制（H，Hexadecimal），基本符号0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F

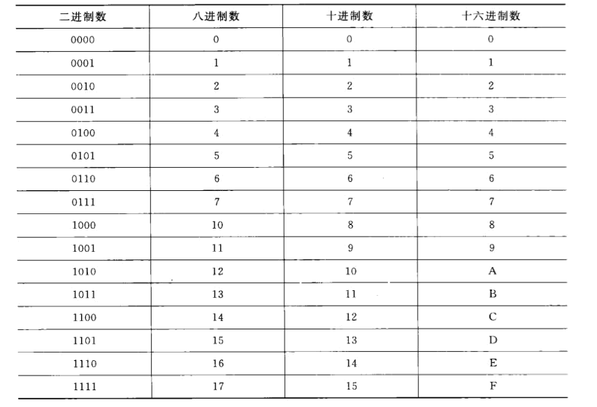
进制之间的转换

进制之间的转换，可以分为二进制转其他进制，或者反过来，其他进制转二进制。
在转换之前，需要了解原码、反码、补码

原码、反码、补码

  1. 原码，就是符号位加上数字的二进制数表示的形式。

    🌰 举例子，Java中byte（1一个字节，长度8位）类型：

    1
    2
    +7(D)的原码：0000 0111
    -7(D)的原码：1000 0111

  2. 反码，正数情况下，与原码一致；负数情况下，符号位不变，在原码的基础每一位取反。

    🌰 举例子，Java中byte（1一个字节，长度8位）类型：

    1
    2
    +7(D)的原码：0000 0111，反码：0000 0111
    -7(D)的原码：1000 0111，反码：1111 1000

  3. 补码，正数情况下，与原码一致；负数情况下，在反码基础加1

    🌰 举例子，Java中byte（1一个字节，长度8位）类型：

    1
    2
    +7(D)的原码：0000 0111，反码：0000 0111，补码：0000 0111
    -7(D)的原码：1000 0111，反码：1111 1000，补码：1111 1001

总结，正数情况下，三码相同；负数情况下，反码符号位不变，其余位取反，补码在反码加1。

二进制转其他(R)

  1. 二进制转十进制 
    1
    1011(B) = 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 11(D)
  2. 二进制转八进制

    整数部分从低位到高位方向每3位改写成八进制数替换，最后不足3位时在高位补0。
    小数部分从高位向低位方向每3位改写成八进制数替换，最后不足3位时在低位补0。

    1
    1011(B) = 001 011 = 13(O)
  3. 二进制转十六进制

    整数部分从低位到高位方向每4位改写成十六进制数替换，最后不足4位时在高位补0。
    小数部分从高位向低位方向每4位改写成十六进制数替换，最后不足4位时在低位补0。

    1
    10110(B) = 1011 0 = B0(H)

其他(R)转二进制

反过来即可

十进制正数、负数转其他进制(R)

要将整数部分和小数部分分别进行转换，这两部分的转换规则是不同的。

  1. 整数部分的转换规则：

    反复除以基数R，直到余数为0为止，每次除法得到的余数从下到上依次排列即是R进制数最终结果。

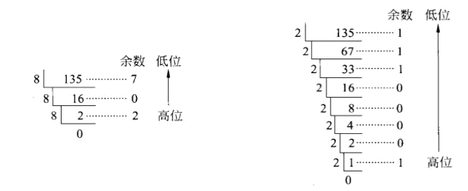
所以135(D) = 207(O) = 10000111(B)

  1. 小数部分的转换规则：

    反复乘以基数R，得到的数字小数部分继续与基数R相乘，直到结果的小数部分为0为止，
    每次相乘得到的中间结果从高到低依次排列即是最终结果。

1
2
3
4
0.6875 * 2 = 1.375  整数部分=1  （高位）
0.375 * 2 = 0.75    整数部分=0    ↓
0.75 * 2 = 1.5      整数部分=1    ↓
0.5 * 2 = 1.0       整数部分=1  （低位）

所以0.6875(D) = 0.1011(B)。

1
2
0.6875 * 8 = 5.5    整数部分=5  （高位）
0.5 * 8 = 4.0       整数部分=4  （低位）

所以0.6875(D) = 0.54(O)。

有一种情况就是每次乘积后的小数部分永远得不到0，这种情况下得到的是个近似值。

什么是定点数

定点数，就是固定小数点的位置，小数点前后的数字用二进制存储在计算机中的一种方式。

🌰 举例子，Java中byte（1一个字节，长度8位）类型，假设约定整数部分占4位，小数部分占4位。

1
2.1(D) = 0010 0001(B)

总结，定点数逻辑简单，但是有一个弊端，按照以上的约定规则整数最大数为15(D) = 1111(B)，小数部分最小为0.9375(D) = 0.1111(b)。
表示范围有限，假设想表示更大的数：

  1. 扩大字节长度，占2个以上字节。这种方式占用计算机内存
  2. 扩大整数部分占用位数，小数点右移。比如整数占5位。这种方式会降低小数精度。
    相反，想表示更小的数，也会有这样的问题。

什么是浮点数

浮点数，就是小数点的位置不是固定的，小数点前后的数字用二进制存储在计算机中的一种方式。

科学计数法

浮点数是采用科学计数法的方式来表示的。

1
2
3
1015(D) = 0.1015 * 10^4 (D) 
1015(D) = 1.015 * 10^3 (D)
1015(D) = 10.15 * 10^2 (D)

这样的形式，小数点就是浮动。根据以上的表示格式，总结出：

1
V = (-1)^S * M * R^E

其中各个变量的含义如下：

  • S：符号位，取值 0 或 1，决定一个数字的符号，0 表示正，1 表示负
  • M：尾数，用小数表示，例如前面所看到的 1.015 * 10^3，1.015 就是尾数
  • R：基数，表示十进制数 R 就是 10，表示二进制数 R 就是 2
  • E：指数，用整数表示，例如前面看到的 10^-1，-1 即是指数

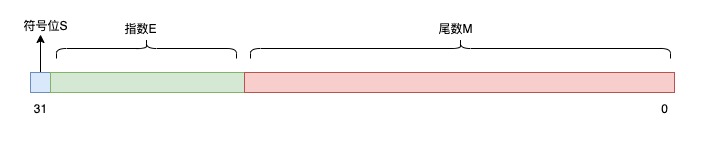
浮点数标准

根据以上的公式，指数和尾数分配规则不同，产生结果也不同。，因此有了浮点数标准。

单精度浮点数float：32 位，符号位 S 占 1 bit，指数 E 占 8 bit，尾数 M 占 23 bit

双精度浮点数double：64 位，符号位 S 占 1 bit，指数 E 占 11 bit，尾数 M 占 52 bit

为了使其表示的数字范围、精度最大化，浮点数标准还对指数和尾数进行了规定：

  • 尾数 M 的第一位总是 1（因为 1 <= M < 2），因此这个 1 可以省略不写，它是个隐藏位，
    这样单精度 23 位尾数可以表示了 24 位有效数字，双精度 52 位尾数可以表示 53 位有效数字
  • 指数 E 是个无符号整数，表示 float 时，一共占 8 bit，所以它的取值范围为 0 ~ 255。
    但因为指数可以是负的，所以规定在存入 E 时在它原本的值加上一个中间数 127，这样 E 的取值范围为 -127 ~ 128。
    表示 double 时，一共占 11 bit，存入 E 时加上中间数 1023，这样取值范围为 -1023 ~ 1024。

除了规定尾数和指数位，还做了以下规定：

  1. 指数 E 非全 0 且非全 1：规格化数字，按上面的规则正常计算
  2. 指数 E 全 0，尾数非 0：非规格化数，尾数隐藏位不再是 1，而是 0(M = 0.xxxxx)，这样可以表示 0 和很小的数
  3. 指数 E 全 1，尾数全 0：正无穷大/负无穷大（正负取决于 S 符号位）
  4. 指数 E 全 1，尾数非 0：NaN(Not a Number)

标准浮点数的表示

有了统一的浮点数标准，我们再把 25.125 转换为标准的 float 浮点数：

  • 整数部分：25(D) = 11001(B)
  • 小数部分：0.125(D) = 0.001(B)

用二进制科学计数法表示：

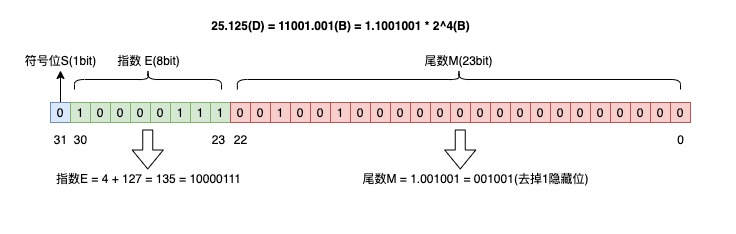
1
25.125(D) = 11001.001(B) = 1.1001001 * 2^4(B)

所以 S = 0，尾数 M = 1.001001 = 001001(去掉1，隐藏位)，
指数 E = 4 + 127(中间数) = 135(D) = 10000111(B)。 填充到 32 bit 中，如下：

浮点数精度丢失

🌰 举例子，0.2(D)用浮点数表示，在转二进制时发现乘以2陷入循环，而浮点数的尾数长度有限，
因此不能准确表示0.2，发生精度丢失情况。

1
2
3
4
5
6
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0（发生循环）
...

浮点数的范围和精度

单精度浮点数 float 为例。

它能表示的最大二进制数为 +1.1.11111…1 * 2^127（小数点后23个1）， 而二进制 1.11111…1 ≈ 2，
所以 float 能表示的最大数为 2^128 = 3.4 * 10^38，
即 float 的表示范围为：-3.4 * 10^38 ~ 3.4 * 10 ^38。

float 能表示的最小二进制数为 0.0000….1（小数点后22个0，1个1），用十进制数表示就是 1/2^23。

用同样的方法可以算出，
double 能表示的最大二进制数为 +1.111…111（小数点后52个1） * 2^1023 ≈ 2^1024 = 1.79 * 10^308，
所以 double 能表示范围为：-1.79 * 10^308 ~ +1.79 * 10^308。

double 的最小精度为：0.0000…1(51个0，1个1)，用十进制表示就是 1/2^52。

BigDecimal

从上得知，浮点数存在精度丢失的问题，那么在开发过程中，一般使用BigDecimal确保精度。

BigDecimal 使用注意事项

  • 在使用BigDecimal时，为了防止精度丢失，推荐使用它的BigDecimal(String val)构造方法
    或者BigDecimal.valueOf(double val)静态方法来创建对象。
  • 使用divide方法的时候尽量使用divide(BigDecimal divisor, int scale, RoundingMode roundingMode)，
    其中scale表示要保留几位小数，roundingMode 代表保留规则，并且RoundingMode参数不要选择UNNECESSARY，
    否则很可能会遇到ArithmeticException（无法除尽出现无限循环小数的时候）。
  • 大小比较使用compareTo方法

BigDecimal如何防止精度丢失

add源码分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
private static BigDecimal add(final long xs, int scale1, final long ys, int scale2) {
    long sdiff = (long) scale1 - scale2;
    if (sdiff == 0) {
        return add(xs, ys, scale1);
    } else if (sdiff < 0) {
        int raise = checkScale(xs,-sdiff);
        long scaledX = longMultiplyPowerTen(xs, raise);
        if (scaledX != INFLATED) {
            return add(scaledX, ys, scale2);
        } else {
            BigInteger bigsum = bigMultiplyPowerTen(xs,raise).add(ys);
            return ((xs^ys)>=0) ? // same sign test
                new BigDecimal(bigsum, INFLATED, scale2, 0)
                : valueOf(bigsum, scale2, 0);
        }
    } else {
        int raise = checkScale(ys,sdiff);
        long scaledY = longMultiplyPowerTen(ys, raise);
        if (scaledY != INFLATED) {
            return add(xs, scaledY, scale1);
        } else {
            BigInteger bigsum = bigMultiplyPowerTen(ys,raise).add(xs);
            return ((xs^ys)>=0) ?
                new BigDecimal(bigsum, INFLATED, scale1, 0)
                : valueOf(bigsum, scale1, 0);
        }
    }
}

这是重点，逐行分析：

  1. checkScale方法检查sdiff从long转int类型是否相等，不想等则检查是否超出Integer.MAX_VALUE，以及检查ys是否为0，返回sdiff的int值
  2. longMultiplyPowerTen方法，把ys扩大，乘以10的raise次方
  3. 最终变成long类型的整型数相加

结论

BigDecimal在计算时，实际会把数值扩大10的n次倍，变成一个long型整数进行计算，
整数计算时自然可以实现精度不丢失。同时结合精度scale，实现最终结果的计算。